رگرسیون لاسو: توضیحات ساده و قابل فهم

در جهان امروز، حجم زیادی از داده‌ها تولید یا در حال تولید است. بررسی و تحلیل این حجم عظیم از مشاهدات و متغیرها نیازمند زمان و هزینه زیادی است. بنابراین، ساده‌سازی مسائلی که به نظر پیچیده می‌آیند، در تجزیه و تحلیل داده‌ها بسیار ضروری است. احتمالاً دنیا به پیچیدگی فکر شده کمتر از آن است و می‌توان با تعداد کمتری از متغیرها نتایج بهتری در تحلیل داده‌ها به دست آورد. به عنوان مثال، با توجه به اینکه انسان حدود ۳۰ هزار ژن دارد، منتظریم تعداد کمتری از این ژن‌ها با بیماری سرطان مرتبط باشند.

در زمینه هنر نیز، می‌توانیم انتظار داشته باشیم که برای حدس زدن سلیقه یک بیننده فیلم، نتایج نظرسنجی از او برای تنها حدود ۵۰ تا ۶۰ فیلم کافی باشد. این توقعات براساس سادگی قوانین حاکم بر دنیا و جامعه بیان می‌شود. در این راستا، رگرسیون لاسو یک ابزار کارآمد در تحلیل‌های چندمتغیره خطی است.

استفاده از رگرسیون لاسو به ما کمک می‌کند تا روش مناسب برای مدل‌سازی متغیر پاسخ با استفاده از کمترین و بهترین تعداد متغیرهای مستقل را پیدا کنیم. نام "لاسو" از واژه‌ای به معنای طناب و کمند انداختن گرفته شده است، و این روش هدف دارد با کمند زدن متغیرهای مناسب، آن‌ها را از سایر متغیرها جدا کرده و یک مدل ساده‌تر و کارآمدتر ارائه دهد.

رگرسیون لاسو

رگرسیون خطی یک مدل آماری است که فرض می‌کند ما دارای N مشاهده از نتایج (یا متغیر پاسخ y) و p متغیر پیشگو (یا ویژگی) هستیم. هدف اصلی این مدل، پیش‌بینی متغیر پاسخ بر اساس داده‌های مشاهده شده از متغیرهای پیشگو است.

این مدل رگرسیون خطی نیز می‌تواند برای پیش‌بینی مقادیر متغیر پاسخ برای داده‌های تست (داده‌هایی که در فرآیند مدل‌سازی حضور نداشته‌اند) استفاده شود.

در زمینه رگرسیون خطی، ما از یک مدل ریاضی برای نمایش ارتباط بین متغیرهای پاسخ و پیشگو استفاده می‌کنیم. این مدل ارتباط را به صورت زیر مدل می‌کند:

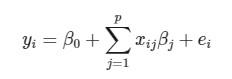
که در آن $${\beta }_0$$ تا $${\beta }_p$$ پارامترهای نامعلوم و نامشخص مدل خطی هستند. به این پارامترها گاهی ضرایب مدل رگرسیونی نیز می‌گویند. در روش کمترین مربعات خطا تابع هدف برای برآورد پارامترها به صورت زیر معرفی می‌شود:

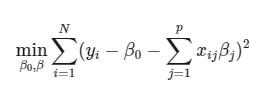
در بیشتر موارد، برآورد برای پارامترهای این مدل صفر نخواهد بود و هیچ  متغیری بدون اثر در مدل بدست نمی‌آید. پس همه متغیرها در مدل نقش داشته و برای پیش‌بینی مقدارهای متغیر پاسخ به کار گرفته می‌شوند. اگر رابطه مربعات خطا را به صورت برداری بنویسیم، با استفاده از مشتق‌گیری می‌توان برآورد پارامترها را به کمک کمترین مقدار مربعات خطا بدست آورد.

در نتیجه پارامترها که با $$\hat{\beta }$$ نشان داده می‌شوند، مطابق با رابطه زیر حاصل خواهند شد:

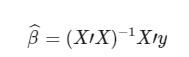
توجه داشته باشید که ماتریس X دارای ابعاد $$N\times p$$ است. حال تصور کنید که تعداد متغیرها (p) بزرگتر از N باشد. در اینجا مقدارها را به صورت p=5 و N=3 تصور کرده و سعی می‌کنیم محاسبات مربوط به رابطه بالا را انجام دهیم. اگر سطرهای ماتریس X را مشاهدات و ستون‌ها را متغیرها در نظر بگیریم، می‌توان برای مثال X را به صورت زیر نوشت:

در نتیجه «ترانهاده» (Transpose) ماتریس X که با $$X\prime$$ نشان داده می‌شود، با تغییر سطرها و ستون‌های آن محاسبه شده و سپس عبارت $$\left(X\prime X\right)$$ را بدست می‌آوریم.

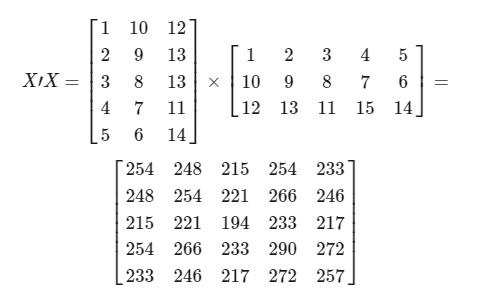
اما با توجه به دترمینان ماتریس حاصلضرب ($$|X\prime X|\approx 0$$) متوجه می‌شویم که این ماتریس معکوس پذیر نیست و امکان برآورد پارامترها برای چنین مدلی وجود ندارد. پس باید با استفاده از روش‌هایی خاص، تعداد متغیرها را کاهش داده یا از شیوه کمینه‌سازی مربعات خطا صرف نظر کنیم.

ولی در رگرسیون لاسو (عمل‌گر گزینش و انقباض کمترین قدرمطلق - Least Absolute Shrinkage and Selection Operator) که توسط رابرت تیب‌شیرانی (Robert Tibshirani) در سال 1996 معرفی شد، روش اول یعنی کاهش بعد متغیرها به کار رفته و از کمینه‌سازی مجموع مربعات تغییر یافته استفاده می‌شود. به این ترتیب با استفاده از یک تابع جریمه (Penalty) روی جمع قدرمطلق ضرایب مدل رگرسیونی، تعداد پارامترها کنترل می‌شود.

در این حالت، مجموع مربعات خطای رگرسیونی لاسو به صورت زیر نوشته می‌شود:

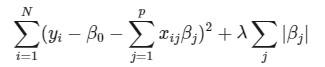
در این رابطه $$\lambda$$ پارامتر تنظیم کننده است، به این معنی که اگر مقدارش برابر با صفر باشد، مدل به رگرسیون عادی تبدیل شده و همه متغیرها در آن حضور خواهند داشت و اگر مقدار آن افزایش یابد تعداد متغیرهای مستقل در مدل کاهش خواهند یافت. بنابراین با انتخاب $$\infty$$ برای $$\lambda$$ عملاً هیچی متغیری در مدل وجود ندارد. تعیین مقدار برای این پارامتر معمولا توسط روش‌ «اعتبارسنجی متقابل» (Cross Validation) انجام می‌شود.

در این حالت، مجموع مربعات خطای رگرسیونی لاسو به صورت زیر نوشته می‌شود:

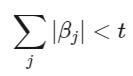
در این رابطه $$\lambda$$ پارامتر تنظیم کننده است، به این معنی که اگر مقدارش برابر با صفر باشد، مدل به رگرسیون عادی تبدیل شده و همه متغیرها در آن حضور خواهند داشت و اگر مقدار آن افزایش یابد تعداد متغیرهای مستقل در مدل کاهش خواهند یافت. بنابراین با انتخاب $$\infty$$ برای $$\lambda$$ عملاً هیچی متغیری در مدل وجود ندارد. تعیین مقدار برای این پارامتر معمولا توسط روش‌ «اعتبارسنجی متقابل» (Cross Validation) انجام می‌شود.

نکته: ممکن است به جای استفاده از پارامتر $$\lambda$$، شرطی که باعث کنترل تعداد متغیرهای مستقل می‌شود را به صورت زیر نوشت که در آن t پارامتر تنظیم کننده مدل است. ولی به هر حال باید توجه داشت که تعداد پارامترها براساس مجموع قدرمطلق ضرایب کنترل می‌شوند.

$$\sum _j|{\beta }_j|<t$$

برای اجرای رگرسیون لاسو، بسته‌هایی در زبان‌های R و Python وجود دارند که در این نوشتار فقط به بررسی و اجرای یکی از آن‌ها در زبان برنامه‌نویسی R می‌پردازیم. «بسته» (Package) محاسباتی lars برای اجرای رگرسیون Lasso در محیط R به کار گرفته می‌شود. کافی است این بسته را بارگذاری کنید تا به توابع مربوط به رگرسیون Lasso دسترسی داشته باشید. در این بسته «مجموعه داده‌های دیابت» (Diabetes Dataset) نیز قرار دارد که از آن برای ایجاد مدل رگرسیونی کمک می‌گیریم.

مثال

ابتدا مجموعه داده دیابت را بارگذاری می‌کنیم. این کار به کمک دستورات زیر امکان پذیر است.

library(lars)
data(diabetes)
attach(diabetes)

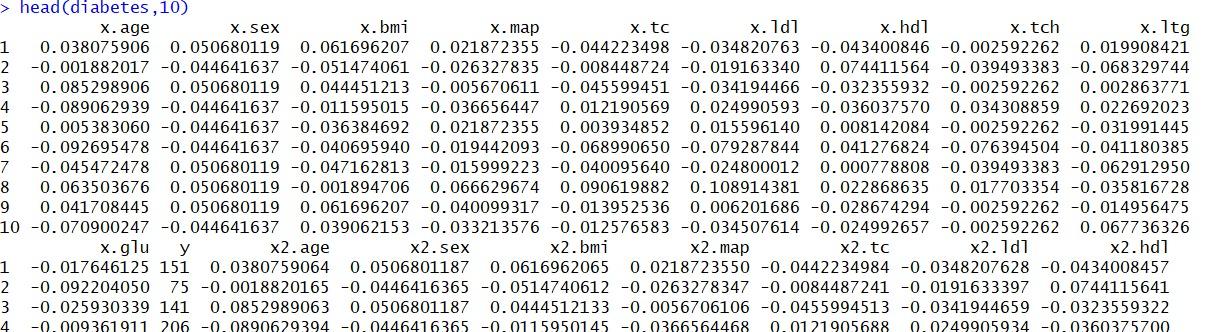
با استفاده از دستور $$head(diabetes,10)$$ ده سطر اول از این داده‌ها مطابق با تصویر زیر نمایش داده می‌شود.

همانطور که در تصویر مشخص است، متغیرهای مستقل با پیشوند x و متغیر پاسخ نیز با y نام‌گذاری شده‌اند. در این مثال از متغیرهای دیگر مانند گروه x2 و ... در ایجاد مدل استفاده نشده است. مشخص است که متغیرهای مستقل، استاندارد شده‌اند یعنی دارای میانگین صفر و واریانس ۱ هستند تا محاسبات به راحتی صورت پذیرند. حال به بررسی کد مربوط به رگرسیون لاسو می‌پردازیم. کدهای زیر به منظور تهیه یک مدل رگرسیونی برای داده‌های دیابت با روش رگرسیون لاسو نوشته شده‌اند.

object <- lars(x,y,type = 'lasso')
object
plot(object)
lassocoef=coef(object)
lassocoef

در خط اول کد، بارگذاری بسته lars صورت گرفته است. دستور lars با توجه به متغیرهای x و y، مدل رگرسیونی لاسو را با پارامتر $$type{=}^{\prime }lass{o}^{\prime }$$ اجرا کرده و خروجی را در object قرار می‌دهد. فرمان plot‌ نیز خروجی تولید شده را به صورت نمودار ظاهر می‌سازد. برآورد پارامترهای مدل در هر مرحله نیز با دستور coef برای متغیر object تولید می‌شود.

خروجی که در متغیر object قرار گرفته را می‌توانید با وارد کردن نام این متغیر (همانطور که در سطر دوم کد دیده می‌شود) مانند تصویر زیر ظاهر کنید.

در خروجی مشخص است که متغیرها، به ترتیبی که در سطر Step دیده می‌شوند به مدل وارد شده‌اند. برآورد پارامترهای مدل در رگرسیون لاسو از طریق الگوریتم‌های بهینه‌سازی، مرحله به مرحله تا رسیدن به کمترین مربعات خطا انجام می‌شود. مقدار «ضریب تعیین» (R-squared) برای مدل ایجاد شده نیز برابر با 0.518 است.

برای مثال در مرحله صفر همه ضرایب (پارامترهای مدل) صفر هستند. در مرحله اول متغیر bmi با شماره ۳ و سپس متغیر ltg‌ با شماره ۹ وارد مدل می‌شوند. همچنین متغیر age با شماره ۱ در مرحله ۱۰ یعنی آخرین مرحله به مدل وارد شده است. متغیر hdl در مرحله ۱۱ خارج سپس وارد مدل شده‌ است. به نظر می‌رسد که این متغیر نباید در مدل در نظر گرفته شود.

برای مشاهده مقدار دقیق پارامترهای مدل از دستور ceof از بسته LARS استفاده می‌‌شود. ولی از آنجایی که مقدار این پارامترها در هر مرحله متفاوت است جدولی از برآورد پارامترها ارائه می‌شود که به صورت زیر خواهد بود.

همانطور که مشخص است، ابتدا همه ضرایب صفر بوده و متغیری که بیشترین همبستگی را با متغیر وابسته داشته وارد مدل شده است. سپس براساس مقدار‌های مختلف $$\lambda$$ متغیرهای جدید به مدل اضافه شده تا آخرین مرحله که همه متغیرها در مدل حضور دارند. مدل مناسب می‌تواند مدلی باشد که در آن مرحله‌ تغییر محسوسی در مقدار مجموع مربعات خطا رخ ندهد. به این ترتیب ضرایب بدست آمده را ملاک تشکیل مدل در نظر می‌گیریم.

برای نمایش تصویری از نحوه ورود و حدود مقدار پارامترها، از نموداری که توسط دستور مربوط به خط سوم کد ترسیم شده کمک می‌گیریم. . ضمناً در هر مرحله نیز حدود ضرایب استاندارد مدل روی محور عمودی سمت چپ دیده می‌شود. برای مثال ضرایب مدل برای متغیر bmi و ltg در مرحله هفتم تقریبا برابر با ۵۰۰ خواهد بود.

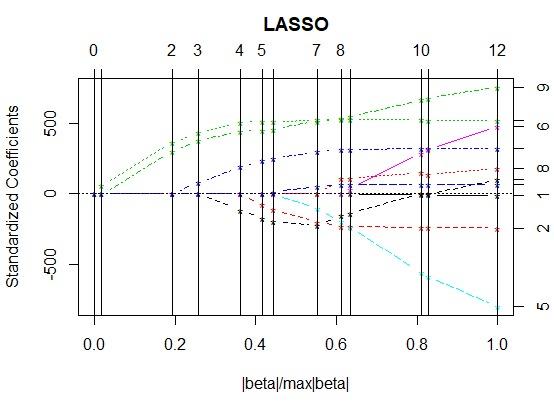
ترتیب ورود ضرایب در محور افقی نمودار بالا مشخص است، همچنین مقادیر پارامترها در مراحل مختلف بر روی محور عمودی سمت چپ قابل مشاهده هستند. محور عمودی سمت راست نیز شماره پارامترها را نمایش می‌دهد. در قسمت پایین نمودار، نسبت مقدار قدرمطلق هر ضریب به حداکثر قدرمطلق آن یعنی |β|max|، در محور افقی قابل مشاهده است.

برای درک بهتر این موضوع و مطالعه موارد مشابه، پیشنهاد می‌شود که به آموزش‌های زیر نیز مراجعه کنید: